2 Didaktische Empfehlungen

2.1 Material & Einführung

Zur Einführung des Spiels empfiehlt sich die Variante mit Feldlänge 10 (oder 15) mit einer überschaubaren maximalen Legezahl von zwei Plättchen (siehe Abschnitt 1.3.1). Der Grund ist ein pragmatischer:

Bevor die Spielpartner gezielt nach einer Gewinnstrategie suchen, also während des noch freien Experimentierens, ist das Ereignis-Fenster zwischen Spiel-Eröffnung und dem Erkennen der vorletzten Gewinnposition wenig ergiebig. Das Augenmerk kann erst in späteren Phasen hierauf gerichtet werden, wenn zunehmend mehr Bewusstheit und Zielorientierung ins Spiel kommen wird. Daher sollten die anfänglichen Spieldurchgänge nicht zu viel Zeit durch zu lange Feldlängen absorbieren. Eine Feldlänge von 10 ermöglicht auch eher einen gewissen Überblick sowie Erinnerungsleistungen (»Eben hatte ich doch auch schon mal die 4 …!«).

Es hat sich immer wieder bewährt, das Spiel zunächst einmal entweder mit einem Kind vor der ganzen Klasse vorzuspielen, oder als Lehrperson alleine gegen die ganze Klasse, was einen zusätzlichen Motivationseffekt mit sich bringen kann, weil die Lehrperson ja in Kenntnis der Strategie erwartbar gewinnen wird.

Man kann dazu ein Stück Tapetenbahn mit aufgezeichnetem Spielfeld nutzen, um tatsächlich mit haptischen, analogen Erfahrungen zu beginnen (abgesehen vom unten beschriebenen Vorteil …). Damit alle Kinder die Spielregel lernen und verinnerlichen, müssen sie zunächst einige »Probespiele« erleben. Die Lehrerin kann dazu gegen das eine oder andere Kind spielen oder wie gesagt gegen die ganze Klasse – in der Frontalphase für alle sichtbar, damit sich die Spielregeln einprägen können.

2.2 Behutsame Fokussierung

Im Hinblick auf das mittelfristige Unterrichtsziel, eine Gewinnstrategie herauszufinden, gibt es dann zwei prinzipielle Vorgehensweisen. Beiden gemeinsam ist, dass die Kinder nach der Frontalphase und nachdem die Spielregeln verstanden sind, zu zweit auf eigenen Spielplänen spielen. Für beide Varianten gibt es pro & contra-Argumente.

Variante A

Man lässt die Kinder im freien Spiel agieren, solange bis erste Beobachtungen formuliert werden (etwa dass die 7 eine wichtige Rolle spielt). Alsdann erfolgt (mithilfe entsprechender Impulse) entweder eine Ermunterung, noch mehr zu entdecken, oder es wird (erst dann) verraten, dass es eine Gewinnstrategie gibt, die es nun zu entdecken gilt.

Bei diesem Vorgehen wird viel Wert auf das sog. freie Spiel gelegt, ein wichtiges pädagogisches Argument u. a. aus der Spieltheorie. Oft beobachtete Nachteile: Es kann u. U. recht lange dauern, bis die erwarteten Effekte des Stutzens und der ersten Vermutungen eintreten. Derweil spielen die Kinder nicht selten recht oberflächlich und planlos, legen die Plättchen hektisch auf das Spielfeld und achten vorrangig auf die Spielstände (»Wer hat wie oft gewonnen?«) – was ja im Hinblick auf das Ziel der Einheit eigentlich völlig nebensächlich ist. Dennoch kostet diese Phase unweigerlich Konzentration, die dann hinterher für die fokussierte Auseinandersetzung mit dem eigentlichen Kern der Sache fehlt. Gerade in den ersten Grundschulklassen kann dies die Kinder schnell an ihre Grenzen führen.

Variante B

Bevor die Kinder in die Partnerarbeit gehen, wird ihnen explizit mitgeteilt (Zielorientierung), dass es eine Gewinnstrategie gibt, die es nun zu suchen gilt.

Diese Variante beginnt mit einer transparenten Zielorientierung. Das nimmt den Kindern nicht die konkreten Spielerfahrungen, denn auch in diesen Fällen zeigen sie in der Regel große Ausdauer (20 bis 30 Durchgänge sind keine Seltenheit). Und die ersten Versuche sind auch noch ähnlich planlos wie in der Variante A.

Aber die Wahrnehmungrichtung ist bereits fokussiert: Die Kinder wissen, um was es anschließend gehen wird. Und so können sie selbst den Zeitpunkt bestimmen, wann eine bewusstere, zielorientierte Auseinandersetzung einsetzt. Weiterer Vorteil: Die Spiele haben weniger einen Wettkampf-Charakter, bei dem man gegeneinander spielt. Im Rahmen der Zielorientierung wird es gar als ausdrücklicher Auftrag formuliert, dass man gemeinsam nach der Gewinnstrategie fahnden soll. Dann spielt es eben auch für viele Kinder eine untergeordnete Rolle, ob es 6:2 oder 6:5 steht.

2.3 Risiko …!

Herausfordern

In eigenen Unterrichtserprobungen hat einer der Autoren stets so begonnen, dass er nach dem Erklären der Spielregel gegen die gesamte Klasse antrat. Im Hinblick auf den Motivationsaufbau zum Aufsuchen einer Gewinnstrategie ist es dabei hilfreich, wenn man diese Probespiele »gegen« die Klasse allesamt gewinnt. Denn dann wird das entweder den Kindern von alleine schon suspekt vorkommen, sodass sie einen »Trick« dahinter vermuten. Oder man kann bereits hier die plausible Zielorientierung liefern, indem man zugibt, einen Wissensvorsprung zu haben, den es aufzuklären gilt.

Motivieren

Das wird viele Kinder motivieren, dieses Wissen ebenfalls zu erwerben, v. a. wenn man ihnen in Aussicht stellt, dass auch sie dann jedes Spiel gewinnen würden – vorausgesetzt natürlich, sie spielen es gegen jemanden, der die Strategie nicht kennt.

Eine Lehrerin hat seinerzeit berichtet, dass sie danach Anrufe von zahlreichen Eltern erhalten habe, die darüber berichteten, dass die Kinder jeden, aber auch jeden, der ihnen zu Hause über den Weg laufen würde, zum Nim-Spiel aufforderten, um dann ihren »Trick« auszuspielen und sämtliche Erwachsene zu besiegen. Ein beeindruckendes Beispiel für den Motivationsfaktor Könnens-Erfahrung.

Aber zurück zum möglichen Risiko: Als Lehrperson kennt man ja die Gewinnstrategie (mit 1 Plättchen beginnen und dann 4 und 7 anzielen), was soll da also schief gehen? Dass es vorkommt, dass die Kinder die Farben der Plättchen mit Ihnen tauschen wollen, kann man ja ganz souverän akzeptieren. Aber den Kindern wird es vermutlich auch bald auffallen, dass immer nur die Lehrperson beginnt.

»Souverän« bleiben

Auch in dieser Situation kann man Souveränität ausstrahlen und »selbstverständlich« auch mal die Klasse beginnen lassen. Denn wenn die Kinder dann als erstes 2 Plättchen legen, ist einem ja die 4 und damit der Sieg wieder sicher. Beginnen die Kinder allerdings mit 1 Plättchen (Achtung: Gewinnposition!), dann ist die Feldlänge 10 i. A. lang genug, dass man entweder vielleicht doch noch die 4 erreichen kann, oder zumindest die 7.

Aber gleichzeitig ist die Feldlänge 10 auch so kurz, dass das eben auch mal schief gehen kann und die Lehrperson verliert. In dem Fall ist sicher eine kleine »didaktische Schummelei« erlaubt: Die Lehrperson stutzt, zeigt sich irritiert und entschuldigt sich, »weil ich gerade etwas unkonzentriert war«. Weitere Probespiele mag man dann ja wieder gewinnen.

Und selbst im Worst Case, dass die Kinder grundsätzlich und mit 1 Plättchen beginnen wollten, hat man damit noch lange nicht die Gewinnstrategie enttarnt, sondern nur einen ganz kleinen Teil. Das Risiko, damit zwischendurch doch immer mal wieder verlieren zu können, ist jedenfalls zu hoch und rechtfertigt auch nicht den Begriff der Gewinnstrategie, den man ja auch als solchen den Kindern transparent machen sollte.

2.4 Vorschnell vermeintlich am Ziel

Das siebte Feld als relevante Position erkannt zu haben, führt, ein häufig zu beobachtendes Phänomen, nicht selten zur (vorschnellen) Zufriedenheit. Man hält die Aufgabe für gelöst, die Gewinnstrategie für erkannt, was aber angesichts der eingangs genannten Definition des Begriffs »Gewinnstrategie« leider noch nicht der Fall ist.

Wie aber motiviert man Kinder an dieser Stelle dazu, dennoch »dranzubleiben« und weiter zu denken? Die Rückmeldung »Das ist noch nicht alles« ist dazu weniger geeignet, weil sie das Augenmerk auf Defizite lenkt und wenig Mut macht. Ein erfahrungsgemäß wirksameres Vorgehen ist das folgende:

Hier kommt der o. g. Spielplan in Form der angesprochenen Tapetenbahn wieder in den Blick: Für die Kinder ist es durchaus plausibel, die Bahn nach der Erkenntnis der Position 7 hinter dieser Position nach unten weg zu falten; schließlich ist ja bei der 7 »alles klar«.

Der Frage »Wie kommt man denn auf die 7?« lässt sich nachgehen, indem bislang gewohnte Spiel-Erfahrungen weiter aktiviert werden; es bedarf keiner neuen Überlegungen. Auch Kinder mit Lernschwierigkeiten können hier wie zuvor mittun. Vergleichsweise schneller als zuvor bei der 7 können die Kinder auf der verkürzten Bahn die Bedeutung der Position 4 herausfinden. Und noch zügiger wird die 1 erkannt, wenn der Spielplan (nun nur noch als nonverbaler Impuls) hinter der 4 umgefaltet wird.

Die wieder entfaltete Tapetenbahn zeigt dann die sichtbaren Knickfalzen (in der Funktion der Rahmen aus Abb. 1.4) – sehr hilfreich für die anschließende Analysen.

2.5 Rolle der Dokumentation

2.5.1 Überblick behalten

Um die Gewinnstrategie herauszufinden, bedarf es einer ganzen Reihe von Spieldurchgängen, denn »die Kinder müssen die Vielfalt der Spielzüge (Operationen) und der Spielpositionen erfassen, die Wirkung der Spielzüge hinsichtlich Gewinn oder Verlust bewerten und ihre eigenen Züge mit denen des Gegners koordinieren« (E. Wittmann, 1982, S. 82). Es ist plausibel, dass insbesondere Grundschüler da schnell den Überblick verlieren. Aber auch Erwachsene wissen sehr schnell nicht mehr, ob sie diesen oder jenen Ansatz oder Zug nicht kurz zuvor so bereits einmal durchgespielt haben.

Nun ist maximale Ökonomie des Spielens und höchste Effektivität der Zielerreichung gar nicht von primärem Interesse. Der spielerische Charakter fragt nicht primär nach dem kürzesten oder elegantesten Weg. Die Vermeidung »unnötiger« Wiederholungen oder Überschneidungen ist aber auch gar nicht das Argument für eine Dokumentation des Tuns. Ihr Wert zeigt sich im Prinzip erst in der folgenden Phase der gemeinsamen Analyse von Hypothesen (vgl. Abschnitt 1.2).

2.5.2 Hypothesen-Prüfung

Die gezieltere Suche nach der Gewinnstrategie führt immer wieder zu Vermutungen und Hypothesen, die überprüft sein wollen. Man kann das tun, indem man einen oder mehrere weitere Spieldurchgänge mit den entsprechenden Parametern durchführt, d. h. sich einige Beispielfälle generiert. Im Unterricht, wo nicht unbegrenzt Zeit zur Verfügung steht (abgesehen von der »Kondition« der Kinder), kann der Bedarf nach weiteren Spielen schon einmal kritisch werden. Alternativ hat sich das folgende Vorgehen bewährt.

2.5.3 Pool an Spielverläufen

In der Phase des freien Explorierens oder der gezielteren Erkundung, für die ca. 15 bis 20 Minuten kalkuliert werden könnten, also während der Partnerarbeitsphase, sollen beide Spielpartner eines oder zwei ihrer »Lieblingsspiele« (Spiele, bei denen sie gewonnen haben oder die sie sonst für bemerkenswert halten) auf einen vorbereiteten großen Spielplan eintragen. Dazu reicht es, die entsprechenden Felder des Spielplans durch rote bzw. blaue Kreuze oder Punkte zu markieren. Das kostet in dieser Phase keine nennenswerte Zeit. Wenn aber alle Spielerpaare so verfahren, dann liegt am Ende der Stunde ein Pool von ca. 30 bis 40 protokollierten Spieldurchläufen vor. Dieser kann dann als Grundlage für die genauere Analyse im Klassenverband dienen.

Werden nun Vermutungen und Hypothesen geäußert – z. B. »Wer anfängt, gewinnt« – dann kann man anhand der gesammelten (und am besten sortierten) Spielverläufe recht gut überprüfen, ob man zunächst ein Gegenbeispiel findet – das wäre der einfachste Weg, um eine Vermutung zu falsifizieren.

Ein Pool von 30 bis 40 Beispielen ist da schon ein relativ guter Ereignisraum. Die Vermutung »Wer anfängt, gewinnt« ließe sich etwa in der Übersicht aus Abb. 2.1 (hier war die Spielfeldlänge 13 bei maximaler Legezahl 2) durch das dort zu findende 8. Spiel widerlegen.

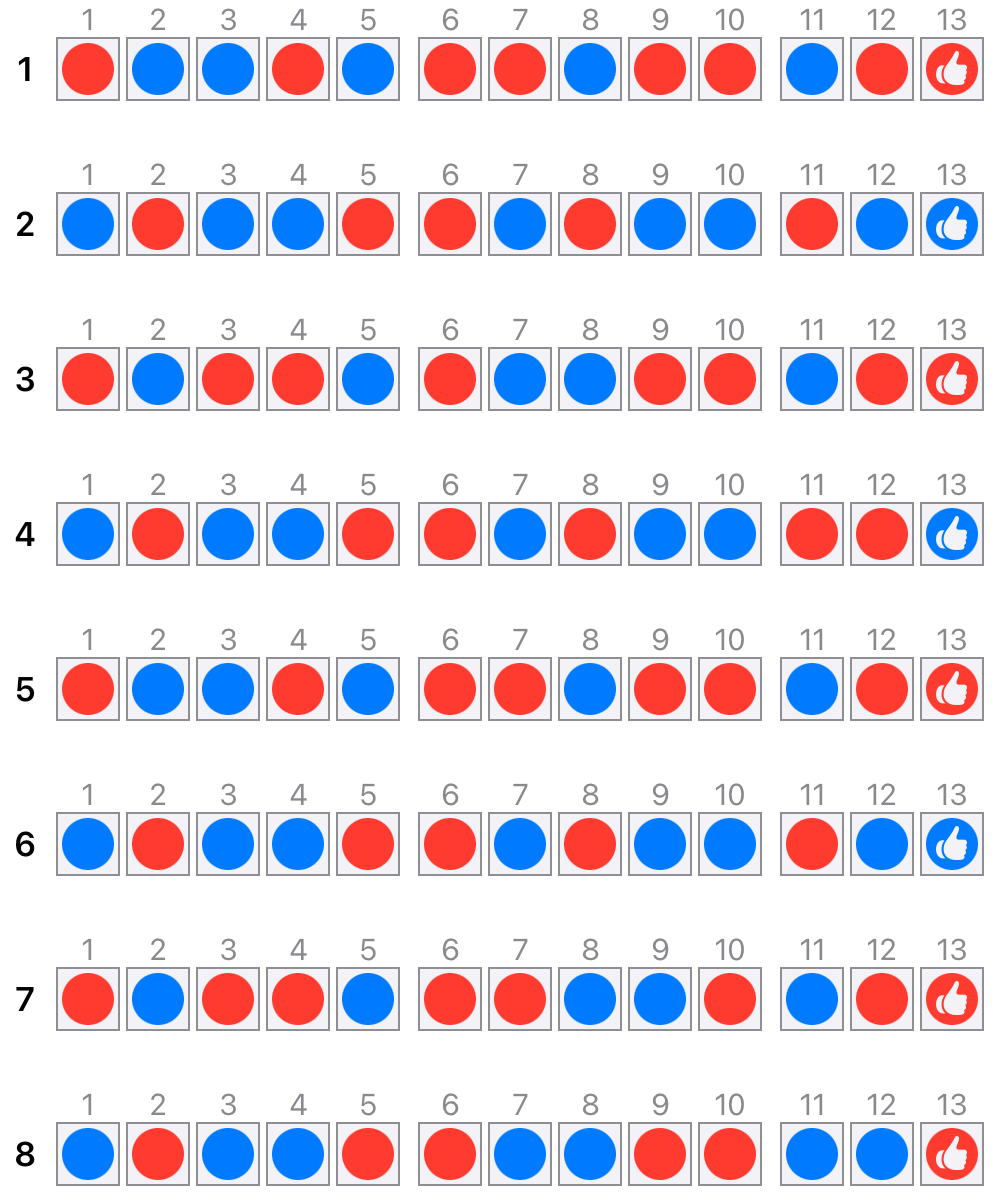
Abb. 2.1: Übersicht über dokumentierte Spielverläufe

Allerdings sollte man die Hypothese auch nicht vorschnell aussortieren, wenn es Beispiele gibt, wo sie zutrifft. Der näher zu untersuchende Grund dafür ist der, dass die genannte Hypothese zwar zutreffend ist, aber noch nicht die ganze Wahrheit enthält (notwendig, aber nicht hinreichend).

Ein solches Tableau muss also aufmerksam interpretiert werden, damit keine Kurzschluss-Folgerungen geschehen. Auch »Wer die 4 legt, gewinnt« (an sich ja eine Gewinnposition) wird durch das 8. Spiel widerlegt. Aber eben nur, weil die Hypothese nur unter der Voraussetzung gilt, dass die Gewinnstrategie konsequent durchgehalten wird, was eben dort nicht zutrifft (die 7 wird hier verpasst, sodass der Spielpartner die 10, die vorletzte Gewinnposition, erreichen kann).

Derartige Analysen und Überprüfungen können nur dann erfolgen, wenn vorherige Spielverläufe dokumentiert und leicht (um-)sortierbar vorliegen. Es würde jedes Gedächtnis überfordern, sich auch nur an die letzten wenigen Spielverläufe zu erinnern. Und wie will man dann mental vergleichen und diese Überlegungen dann auch für andere verständlich kommunizieren? Ein zwingendes Argument für eine adäquate Dokumentationspraxis!

2.6 Rolle der Sprache

Es liegt auf der Hand, dass eine unterrichtliche Umsetzung des Nim-Spiels auch besonders geeignet ist, um allgemeine mathematische Kompetenzen wie das Darstellen, das Kommunizieren, das Problemlösen und das Argumentieren zu fördern – sowohl im Mündlichen als auch beim Verschriftlichen.

Das Sprachgefühl und die aktuelle sprachliche Ausdrucksfähigkeit der Kinder ist noch in der Entwicklung, weshalb der Satz »Jede Mathematikstunde ist auch eine Deutschstunde« insofern relevant ist, als die sprachliche Ausdrucksfähigkeit der Kinder auch im Fachunterricht zu fördern und zu fordern ist (wobei die Sprache der Lehrerin eine Modellfunktion hat!). Eine besondere Aufgabe für eine Lehrperson besteht z. B. darin, die manchmal sehr verkürzten Satzfragmente der Kinder zunächst selbst zu verstehen und einordnen zu können, und dann auch für die ganze Klasse verständlich zu machen. Dieser Bedarf erklärt sich u. a. wie folgt:

• Kinder formulieren zunächst sehr subjektiv aus ihrer individuellen Sicht als »Wissende».

  Sie haben sich mit einem Sachverhalt befasst und dabei vielfältige Detail-Erfahrungen gemacht, die sie nun nicht mehr für erklärungsbedürftig oder erwähnenswert halten (weil sie ihnen klar sind). Dass Außenstehende mehr Redundanz, mehr Einzelheiten benötigen, um die Erklärungen zu verstehen, ist ihnen nicht bewusst.

• (Über-)Motivation und Engagement in der Sache führen auch häufig dazu, dass der Kopf schneller denkt als es der »Sprachausgabe« gelingt, hinterherzukommen.

  Aus einem dadurch entstehenden Wortschwall (in der Fachsprache »Poltern« genannt) kann aber nicht geschlossen werden, dass das Kind den Sachverhalt nicht verstanden hätte. Für Außenstehende aber mag es sich wie ein »verbales Chaos« anhören, dem man überhaupt nicht folgen, geschweige etwas verstehen kann.

• Auch bei Kindern kann man schon einmal »die allmähliche Verfertigung der Gedanken beim Reden« (Kleist, 1978) beobachten.

  Auch wenn der Hinweis »Erst denken, dann reden« gewiss seine Berechtigung hat, so wird das Denken aber auch durch Reden (währenddessen) mitgeformt: Beim »Drauflosreden« ohne schon zu wissen, was man genau sagen und wo man hin will, formieren sich Gedanken, die Bewusstheit wächst und entwickelt den sprachlichen Ausdruck erst zu einer akzeptierten und verständlichen Form.

Bei all dem ist entscheidend, Sprache im Rahmen von Erklärungen, Berichten, Begründungen und Argumentationszusammenhängen nicht einfach nur »geschehen« zu lassen, sondern sie immer wieder auch in den Bewusstseinshorizont der Kinder zu heben – nicht nur mit und durch Sprache kommunizieren, sondern auch über Sprache kommunizieren. Das ist mit aktiver Sprachförderung als eine durchgängige Aufgabe jedweden Unterrichts gemeint.